本节书摘来自异步社区出版社《MATLAB智能算法超级学习手册》一书中的第1章，第1.4节，作者：MATLAB技术联盟 , 高飞 , 许玢更多章节内容可以访问云栖社区“异步社区”公众号查看。

1.4 线性方程组的求解

MATLAB智能算法超级学习手册

线性方程组的求解在日常生活中的应用较多，特别是解决企业规划、任务分配等问题。线性方程组的求解一般分为两类：一类是求唯一解或求特解，另一类是求通解。可以通过由MATLAB求解线性方程组系数矩阵的秩来判断：

若系数矩阵的秩r=n（n为方程组中未知变量的个数），则有唯一解；

若系数矩阵的秩r

线性方程组的通解（无穷解） = 对应齐次方程组的通解 + 非齐次方程组的一个特解，其特解的求法属于解的第一类问题，通解部分属第二类问题。

1.4.1 齐次线性方程组的通解

在MATLAB中，函数null( )用来求解零空间，即满足A·X=0的解空间，实际上是求出解空间的一组基。

格式　z = null　　　　 % z的列向量为方程组的正交规范基，满足Z’×Z=I　　　z =null(A,’r’)　 % z的列向量是方程A·X=0的有理基

解：MATLAB求解程序代码如下。

>> A=[1　2　2　1;2　1　-2　-2;1　-1　-4　-3];      %原始系数矩阵format　rat　　　      %指定有理式格式B=null(A,'r')　　      %求解空间的有理基B =　　　 2　　　　　　　5/3　　 　　　-2　　　　　　 -4/3　　　　　　 1　　　　　　　0　　　 　　　 0　　　　　　　1

或通过最简行得到基：

>>　B=rref(A)B =　　　 1　　　　　　　0　　　　　　 -2　　　　　　 -5/3　　 　　　 0　　　　　　　1　　　　　　　2　　　　　　　4/3　　 　　　 0　　　　　　　0　　　　　　　0　　　　　　　0

则相应地写出线性方程组的通解：

syms　k1　k2 %定义符号变量X=k1*B(:,1)+k2*B(:,2)　　　   %写出方程组的通解% 运行结果显示X =　 2*k1 + (5*k2)/3 - 2*k1 - (4*k2)/3　　　　　　　　k1　　　　　　　　k2 pretty(X)　　       %让通解表达式更精美 +-　　　　　　　 -+ 　|　　　　　5 k2　 | 　|　 2 k1 + ----　 | 　|　　　　　 3　　 | 　|　　　　　　　　 | 　|　　　　　 4 k2　| 　|　- 2 k1 - ----　| 　|　　　　　　3　　| 　|　　　　　　　　 | 　|　　　　k1　　　 | 　|　　　　　　　　 | 　|　　　　k2　　　 | 　+-　　　　　　　 -+

1.4.2 非齐次线性方程组的通解

需要先判断非齐次线性方程组是否有解，若有解，然后求通解，步骤如下。

Step1：判断A·X=b是否有解，若有解，则进行第二步，否则终止求解；

Step2：求A·X=b的一个特解；

Step3：求A·X=0的通解；

Step4：A·X=b的通解等于 A·X=b的通解加上A·X=b的一个特解。

解：在MATLAB中建立脚本M文件：

A=[1　-2　3　-1;3　-1　5　-3;2　1　2　-2];b=[1　2　3]';B=[A b];n=4;RA=rank(A)RB=rank(B)format ratif RA==RB&RA==n　　　    %判断是否有唯一解　 X=A\belseif RA==RB&RA

运行后结果显示为：

RA =　　 2RB =　　 3X =equition no solve

解法一：在MATLAB编辑器中建立M文件：

A=[1　1　-3　-1;3　-1　-3　4;1　5　-9　-8];b=[1 4 0]';B=[A b];n=4;R_A=rank(A)R_B=rank(B)format ratif R_A==R_B&R_A==n　 X=A\belseif R_A==R_B&R_A

运行后结果显示为：

R_A =　　　 2　　　 R_B =　　　 2　　　 Warning: Rank deficient, rank = 2, tol =　3.826647e-15. X =　　　 0　　　 　　　 0　　　 　　　-8/15　　　　　 3/5　　 C =　　　 3/2　　　　　 -3/4　　 　　　 3/2　　　　　　7/4　　 　　　 1　　　　　　　0　　　 　　　 0　　　　　　　1

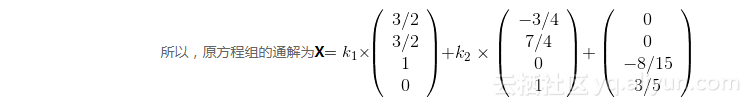
解法二：用rref( )求解：

>> A=[1　1　-3　-1;3　-1　-3　4;1　5　-9　-8];b=[1 4 0]';B=[A b];C=rref(B)　　%求增广矩阵的行最简

运行后结果显示为：

C =　Columns 1 through 5　　　 1　　　　　　　0　　　　　　 -3/2　　　　　　3/4　　 5/4　　 　　　 0　　　　　　　1　　　　　　 -3/2　　　　　 -7/4　　-1/4　　　　　　 0　　　　　　　0　　　　　　　0　　　　　　　0　　　 0

1.4.3 线性方程组的LQ解法

函数symmlq的格式如下：

x = symmlq(A,b)　 %求线性方程组A·X=b的解X。A必须为n阶对称方阵，b为n元列向量。a可以是由afun定义并返回A×X的函数。如果收敛，将显示结果信息；如果收敛失败，将给出警告信息并显示相对残差norm(b-A·X)/norm(b)和计算终止的迭代次数　　symmlq(A,b,tol)　　　　    %指定误差tol，默认值是1e-6　　symmlq(A,b,tol,maxit)　     %maxit指定最大迭代次数　　symmlq(A,b,tol,maxit,M)     %M为用于对称正定矩阵的预处理因子　　symmlq(A,b,tol,maxit,M1,M2)　    %M=M1×M2　　symmlq(A,b,tol,maxit,M1,M2,x0)    %x0为初始估计值，默认值为0　　 [x,flag] = symmlq(A,b,…)　　   %flag的取值为：0表示在指定迭代次数内按要求精度收敛；1表示在指定迭代次数内不收敛；2表示M为坏条件的预处理因子；3表示两次连续迭代完全相同；4表示标量参数太小或太大；5表示预处理因子不是对称正定的　　 [x,flag,relres] = symmlq(A,b,…)    %relres表示相对误差norm(b-A·x)/norm(b) 　　[x,flag,relres,iter] = symmlq(A,b,…)  %_iter_表示计算_x_的迭代次数　　[[x,flag,relres,iter,resvec] = symmlq(A,b,…)  %resvec表示每次迭代的残差：norm(b-A·x0) 　 [x,flag,relres,iter,resvec,resveccg] = symmlq(A,b,…) %resveccg表示每次迭代共轭梯度残差的范数